How to Solve 10is Again Level 8 Multiplying

Algorithm to multiply two numbers

A multiplication algorithm is an algorithm (or method) to multiply ii numbers. Depending on the size of the numbers, different algorithms are used. Efficient multiplication algorithms accept existed since the advent of the decimal organization.

Long multiplication [edit]

If a positional numeral system is used, a natural way of multiplying numbers is taught in schools as long multiplication, sometimes called grade-school multiplication, sometimes called Standard Algorithm: multiply the multiplicand past each digit of the multiplier and then add together upward all the properly shifted results. It requires memorization of the multiplication tabular array for single digits.

This is the usual algorithm for multiplying larger numbers by hand in base 10. A person doing long multiplication on paper will write downwards all the products so add together them together; an abacus-user volition sum the products equally presently as each one is computed.

Example [edit]

This example uses long multiplication to multiply 23,958,233 (multiplicand) by 5,830 (multiplier) and arrives at 139,676,498,390 for the upshot (product).

          23958233 ×         5830 ———————————————       00000000 ( =      23,958,233 ×     0)      71874699  ( =      23,958,233 ×    xxx)    191665864   ( =      23,958,233 ×   800) + 119791165    ( =      23,958,233 × 5,000) ———————————————   139676498390 ( = 139,676,498,390        )        

Other notations [edit]

In some countries such as Germany, the above multiplication is depicted similarly but with the original product kept horizontal and computation starting with the first digit of the multiplier:^[ane]

23958233 · 5830 ———————————————    119791165     191665864       71874699        00000000  ———————————————    139676498390        

Below pseudocode describes the process of above multiplication. It keeps merely one row to maintain the sum which finally becomes the result. Note that the '+=' operator is used to denote sum to existing value and shop functioning (akin to languages such equally Java and C) for compactness.

                        multiply            (            a            [            1            ..            p            ]            ,            b            [            1            ..            q            ]            ,            base            )            // Operands containing rightmost digits at alphabetize 1            product            =            [            1            ..            p            +            q            ]            // Classify space for event            for            b_i            =            one            to            q            // for all digits in b            behave            =            0            for            a_i            =            1            to            p            // for all digits in a            product            [            a_i            +            b_i            -            ane            ]            +=            carry            +            a            [            a_i            ]            *            b            [            b_i            ]            behave            =            product            [            a_i            +            b_i            -            1            ]            /            base            production            [            a_i            +            b_i            -            1            ]            =            product            [            a_i            +            b_i            -            1            ]            modern            base            product            [            b_i            +            p            ]            =            carry            // last digit comes from last carry            return            production          

Usage in computers [edit]

Some fries implement long multiplication, in hardware or in microcode, for various integer and floating-point word sizes. In arbitrary-precision arithmetic, it is common to employ long multiplication with the base set to 2 ^w , where westward is the number of bits in a word, for multiplying relatively small numbers. To multiply two numbers with n digits using this method, one needs about n ² operations. More formally, multiplying two n-digit numbers using long multiplication requires Θ(n ²) single-digit operations (additions and multiplications).

When implemented in software, long multiplication algorithms must deal with overflow during additions, which can be expensive. A typical solution is to stand for the number in a small base of operations, b, such that, for example, viiib is a representable machine integer. Several additions can then be performed before an overflow occurs. When the number becomes also big, nosotros add together part of information technology to the result, or we comport and map the remaining part back to a number that is less than b. This process is called normalization. Richard Brent used this approach in his Fortran package, MP.^[2]

Computers initially used a very similar algorithm to long multiplication in base 2, simply mod processors take optimized circuitry for fast multiplications using more efficient algorithms, at the toll of a more complex hardware realization.^{[ citation needed ]} In base two, long multiplication is sometimes chosen "shift and add", because the algorithm simplifies and only consists of shifting left (multiplying by powers of 2) and adding. Most currently available microprocessors implement this or other similar algorithms (such as Berth encoding) for various integer and floating-point sizes in hardware multipliers or in microcode.^{[ commendation needed ]}

On currently bachelor processors, a scrap-wise shift instruction is faster than a multiply instruction and can be used to multiply (shift left) and separate (shift right) by powers of two. Multiplication by a constant and division by a constant can be implemented using a sequence of shifts and adds or subtracts. For example, there are several ways to multiply by x using only fleck-shift and add-on.

((x << two) + x) << one # Here 10*ten is computed as (10*two^2 + x)*2 (ten << iii) + (x << i) # Here 10*x is computed equally x*ii^iii + 10*2        

In some cases such sequences of shifts and adds or subtracts will outperform hardware multipliers and specially dividers. A sectionalisation by a number of the form ${\displaystyle ii^{northward}}$ or ${\displaystyle 2^{north}\pm 1}$ often can be converted to such a short sequence.

Algorithms for multiplying past paw [edit]

In addition to the standard long multiplication, there are several other methods used to perform multiplication by hand. Such algorithms may be devised for speed, ease of adding, or educational value, particularly when computers or multiplication tables are unavailable.

Grid method [edit]

The filigree method (or box method) is an introductory method for multiple-digit multiplication that is often taught to pupils at master schoolhouse or simple school. It has been a standard part of the national primary school mathematics curriculum in England and Wales since the late 1990s.^[3]

Both factors are cleaved up ("partitioned") into their hundreds, tens and units parts, and the products of the parts are so calculated explicitly in a relatively simple multiplication-merely stage, before these contributions are so totalled to give the final answer in a dissever addition stage.

The calculation 34 × xiii, for case, could be computed using the filigree:

×	30	4
10	300	40
3	90	12

followed by addition to obtain 442, either in a unmarried sum (see right), or through forming the row-by-row totals (300 + 40) + (xc + 12) = 340 + 102 = 442.

This calculation approach (though not necessarily with the explicit grid arrangement) is besides known as the partial products algorithm. Its essence is the calculation of the unproblematic multiplications separately, with all addition being left to the final gathering-up stage.

The grid method can in principle be applied to factors of any size, although the number of sub-products becomes cumbersome equally the number of digits increases. Even so, it is seen as a usefully explicit method to introduce the idea of multiple-digit multiplications; and, in an age when most multiplication calculations are done using a calculator or a spreadsheet, it may in practice exist the but multiplication algorithm that some students volition ever need.

Lattice multiplication [edit]

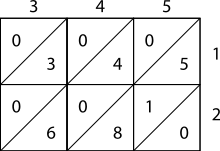
Start, set upwardly the grid by marking its rows and columns with the numbers to be multiplied. So, make full in the boxes with tens digits in the top triangles and units digits on the bottom.

Finally, sum forth the diagonal tracts and conduct as needed to become the respond

Lattice, or sieve, multiplication is algorithmically equivalent to long multiplication. It requires the grooming of a lattice (a filigree drawn on paper) which guides the adding and separates all the multiplications from the additions. Information technology was introduced to Europe in 1202 in Fibonacci's Liber Abaci. Fibonacci described the operation as mental, using his right and left hands to deport the intermediate calculations. Matrakçı Nasuh presented 6 unlike variants of this method in this 16th-century book, Umdet-ul Hisab. It was widely used in Enderun schools across the Ottoman Empire.^[4] Napier'due south bones, or Napier's rods too used this method, as published past Napier in 1617, the yr of his death.

Every bit shown in the instance, the multiplicand and multiplier are written above and to the right of a lattice, or a sieve. Information technology is found in Muhammad ibn Musa al-Khwarizmi'due south "Arithmetic", one of Leonardo's sources mentioned by Sigler, author of "Fibonacci's Liber Abaci", 2002.^{[ commendation needed ]}

• During the multiplication phase, the lattice is filled in with two-digit products of the corresponding digits labeling each row and column: the tens digit goes in the top-left corner.
• During the add-on phase, the lattice is summed on the diagonals.
• Finally, if a comport stage is necessary, the reply as shown along the left and bottom sides of the lattice is converted to normal form past carrying 10's digits as in long add-on or multiplication.

Example [edit]

The pictures on the right bear witness how to calculate 345 × 12 using lattice multiplication. As a more complicated case, consider the picture below displaying the computation of 23,958,233 multiplied by five,830 (multiplier); the result is 139,676,498,390. Notice 23,958,233 is along the tiptop of the lattice and 5,830 is along the right side. The products make full the lattice and the sum of those products (on the diagonal) are forth the left and lesser sides. Then those sums are totaled as shown.

2 3 9 five 8 2 3 iii +---+---+---+---+---+---+---+---+- |1 /|1 /|4 /|2 /|4 /|one /|1 /|1 /| | / | / | / | / | / | / | / | / | 5 01|/ 0|/ five|/ 5|/ 5|/ 0|/ 0|/ 5|/ 5| +---+---+---+---+---+---+---+---+- |i /|2 /|seven /|4 /|half-dozen /|i /|2 /|2 /| | / | / | / | / | / | / | / | / | 8 02|/ vi|/ iv|/ 2|/ 0|/ 4|/ half-dozen|/ 4|/ four| +---+---+---+---+---+---+---+---+- |0 /|0 /|ii /|1 /|2 /|0 /|0 /|0 /| | / | / | / | / | / | / | / | / | 3 17|/ 6|/ 9|/ vii|/ five|/ 4|/ 6|/ 9|/ 9| +---+---+---+---+---+---+---+---+- |0 /|0 /|0 /|0 /|0 /|0 /|0 /|0 /| | / | / | / | / | / | / | / | / | 0 24|/ 0|/ 0|/ 0|/ 0|/ 0|/ 0|/ 0|/ 0| +---+---+---+---+---+---+---+---+- 26 15 13 xviii 17 thirteen 09 00

01 002 0017 00024 000026 0000015 00000013 000000018 0000000017 00000000013 000000000009 0000000000000 ————————————— 139676498390

= 139,676,498,390

Russian peasant multiplication [edit]

The binary method is also known as peasant multiplication, because it has been widely used by people who are classified every bit peasants and thus have not memorized the multiplication tables required for long multiplication.^{[5] [ failed verification ]} The algorithm was in employ in ancient Egypt.^{[six] [7]} Its master advantages are that it can be taught quickly, requires no memorization, and can be performed using tokens, such equally poker fries, if paper and pencil aren't available. The disadvantage is that it takes more steps than long multiplication, so it can exist unwieldy for big numbers.

Clarification [edit]

On paper, write down in one column the numbers you get when y'all repeatedly halve the multiplier, ignoring the rest; in a column beside it repeatedly double the multiplicand. Cross out each row in which the terminal digit of the first number is even, and add together the remaining numbers in the 2nd cavalcade to obtain the production.

Examples [edit]

This example uses peasant multiplication to multiply xi by three to make it at a result of 33.

Decimal:     Binary: eleven   3       1011  eleven v    6       101  110 two          12          10          1100          ane   24       1  11000     ——         ——————     33         100001        

Describing the steps explicitly:

• 11 and 3 are written at the superlative
• 11 is halved (5.5) and 3 is doubled (half dozen). The fractional portion is discarded (5.5 becomes 5).
• 5 is halved (ii.5) and half dozen is doubled (12). The fractional portion is discarded (2.5 becomes ii). The figure in the left column (2) is even, so the figure in the right column (12) is discarded.
• 2 is halved (1) and 12 is doubled (24).
• All not-scratched-out values are summed: 3 + 6 + 24 = 33.

The method works considering multiplication is distributive, and then:

${\displaystyle {\brainstorm{aligned}three\times xi&=3\times (ane\times 2^{0}+one\times 2^{1}+0\times 2^{2}+one\times two^{3})\\&=3\times (1+two+8)\\&=3+6+24\\&=33.\finish{aligned}}}$

A more complicated instance, using the figures from the earlier examples (23,958,233 and 5,830):

Decimal:             Binary: 5830          23958233          1011011000110          1011011011001001011011001          2915  47916466       101101100011  10110110110010010110110010 1457  95832932       10110110001  101101101100100101101100100 728          191665864          1011011000          1011011011001001011011001000          364          383331728          101101100          10110110110010010110110010000          182          766663456          10110110          101101101100100101101100100000          91  1533326912       1011011  1011011011001001011011001000000 45  3066653824       101101  10110110110010010110110010000000 22          6133307648          10110          101101101100100101101100100000000          11 12266615296       1011  1011011011001001011011001000000000 5  24533230592       101  10110110110010010110110010000000000 2          49066461184          10          101101101100100101101100100000000000          one  98132922368       1          1011011011001001011011001000000000000          ————————————          1022143253354344244353353243222210110 (before comport)   139676498390         10000010000101010111100011100111010110        

Quarter square multiplication [edit]

Two quantities can be multiplied using quarter squares past employing the following identity involving the floor function that some sources^{[8] [9]} attribute to Babylonian mathematics (2000–1600 BC).

${\displaystyle \left\lfloor {\frac {\left(ten+y\right)^{two}}{4}}\right\rfloor -\left\lfloor {\frac {\left(x-y\right)^{2}}{four}}\right\rfloor ={\frac {1}{4}}\left(\left(x^{two}+2xy+y^{two}\right)-\left(x^{2}-2xy+y^{2}\right)\right)={\frac {1}{4}}\left(4xy\right)=xy.}$

If one of x+y and x−y is odd, the other is odd too, thus their squares are one modernistic 4, then taking floor reduces both by a quarter; the subtraction then cancels the quarters out, and discarding the remainders does non innovate whatever divergence comparing with the aforementioned expression without the floor functions. Beneath is a lookup table of quarter squares with the remainder discarded for the digits 0 through eighteen; this allows for the multiplication of numbers up to 9×ix.

n	0	1	two	3	iv	5	6	7	8	9	10	11	12	13	14	15	xvi	17	18
⌊n ii/four⌋	0	0	1	2	4	6	9	12	16	20	25	30	36	42	49	56	64	72	81

If, for example, you wanted to multiply 9 past 3, you observe that the sum and difference are 12 and 6 respectively. Looking both those values up on the table yields 36 and 9, the difference of which is 27, which is the product of nine and 3.

Antoine Voisin published a table of quarter squares from i to 1000 in 1817 every bit an aid in multiplication. A larger table of quarter squares from 1 to 100000 was published by Samuel Laundy in 1856,^[10] and a table from one to 200000 by Joseph Blater in 1888.^[11]

Quarter foursquare multipliers were used in analog computers to form an analog signal that was the product of two analog input signals. In this application, the sum and difference of two input voltages are formed using operational amplifiers. The square of each of these is approximated using piecewise linear circuits. Finally the difference of the two squares is formed and scaled by a factor of 1 quaternary using yet some other operational amplifier.

In 1980, Everett 50. Johnson proposed using the quarter square method in a digital multiplier.^[12] To grade the product of two 8-fleck integers, for example, the digital device forms the sum and difference, looks both quantities upwards in a tabular array of squares, takes the difference of the results, and divides by four by shifting two bits to the correct. For 8-scrap integers the table of quarter squares will have 2^nine-1=511 entries (one entry for the total range 0..510 of possible sums, the differences using only the first 256 entries in range 0..255) or 2⁹-1=511 entries (using for negative differences the technique of 2-complements and nine-bit masking, which avoids testing the sign of differences), each entry being 16-flake broad (the entry values are from (0²/4)=0 to (510²/4)=65025).

The quarter square multiplier technique has also benefitted 8-bit systems that do not accept any support for a hardware multiplier. Charles Putney implemented this for the 6502.^[xiii]

Computational complexity of multiplication [edit]

Unsolved problem in information science:

What is the fastest algorithm for multiplication of ii ${\displaystyle n}$ -digit numbers?

Karatsuba multiplication [edit]

For systems that need to multiply numbers in the range of several grand digits, such as computer algebra systems and bignum libraries, long multiplication is too slow. These systems may employ Karatsuba multiplication, which was discovered in 1960 (published in 1962). The heart of Karatsuba's method lies in the ascertainment that ii-digit multiplication can exist washed with merely three rather than the four multiplications classically required. This is an example of what is at present called a separate-and-conquer algorithm. Suppose we want to multiply two two-digit base-m numbers: x _ane m + x ₂ and y ₁ m + y _ii:

1. compute x _ane · y _ane, phone call the result F
2. compute ten _two · y ₂, call the result G
3. compute (x ₁ + x ₂) · (y _one + y ₂), call the result H
4. compute H − F − G, phone call the result K; this number is equal to x ₁ · y ₂ + x _ii · y ₁
5. compute F · m ⁱⁱ + Yard · m + K.

To compute these three products of base grand numbers, we can utilize the aforementioned fob over again, finer using recursion. Once the numbers are computed, we need to add together them together (steps 4 and 5), which takes about n operations.

Karatsuba multiplication has a time complexity of O(n ^log₂3) ≈ O(northward ^one.585), making this method significantly faster than long multiplication. Because of the overhead of recursion, Karatsuba'south multiplication is slower than long multiplication for small values of n; typical implementations therefore switch to long multiplication for small values of n.

Karatsuba'south algorithm was the first known algorithm for multiplication that is asymptotically faster than long multiplication,^[14] and can thus exist viewed as the starting point for the theory of fast multiplications.

Toom–Cook [edit]

Another method of multiplication is called Toom–Melt or Toom-three. The Toom–Cook method splits each number to be multiplied into multiple parts. The Toom–Melt method is ane of the generalizations of the Karatsuba method. A iii-way Toom–Cook can do a size-3N multiplication for the toll of five size-N multiplications. This accelerates the operation by a factor of 9/5, while the Karatsuba method accelerates it past 4/three.

Although using more than and more parts can reduce the time spent on recursive multiplications farther, the overhead from additions and digit direction also grows. For this reason, the method of Fourier transforms is typically faster for numbers with several 1000 digits, and asymptotically faster for even larger numbers.

Fourier transform method [edit]

Demonstration of multiplying 1234 × 5678 = 7006652 using fast Fourier transforms (FFTs). Number-theoretic transforms in the integers modulo 337 are used, selecting 85 equally an 8th root of unity. Base 10 is used in place of base 2 ^w for illustrative purposes.

The basic idea due to Strassen (1968) is to use fast polynomial multiplication to perform fast integer multiplication. The algorithm was fabricated practical and theoretical guarantees were provided in 1971 by Schönhage and Strassen resulting in the Schönhage–Strassen algorithm.^[fifteen] The details are the following: We choose the largest integer w that will not cause overflow during the process outlined beneath. Then we split the two numbers into grand groups of w $.25 equally follows

${\displaystyle a=\sum _{i=0}^{m-i}{a_{i}2^{wi}}{\text{ and }}b=\sum _{j=0}^{m-1}{b_{j}2^{wj}}.}$

We expect at these numbers every bit polynomials in x, where ten = 2 ^w , to get,

${\displaystyle a=\sum _{i=0}^{m-1}{a_{i}x^{i}}{\text{ and }}b=\sum _{j=0}^{1000-1}{b_{j}ten^{j}}.}$

And then we tin say that,

${\displaystyle ab=\sum _{i=0}^{m-1}\sum _{j=0}^{m-1}a_{i}b_{j}x^{(i+j)}=\sum _{k=0}^{2m-2}c_{k}x^{k}.}$

Clearly the to a higher place setting is realized by polynomial multiplication, of 2 polynomials a and b. The crucial step now is to use Fast Fourier multiplication of polynomials to realize the multiplications in a higher place faster than in naive O(yard ⁱⁱ) time.

To remain in the modular setting of Fourier transforms, we look for a ring with a (2m)th root of unity. Hence nosotros practise multiplication modulo N (and thus in the Z/NZ band). Farther, N must exist chosen then that there is no 'wrap around', substantially, no reductions modulo N occur. Thus, the pick of Due north is crucial. For instance, it could be done equally,

${\displaystyle N=ii^{3m}+i.}$

The ring Z/NZ would thus have a (2m)th root of unity, namely 8. Also, it tin be checked that c_grand < N, and thus no wrap around volition occur.

The algorithm has a time complexity of Θ(northward log(n) log(log(north))) and is used in practice for numbers with more than 10,000 to xl,000 decimal digits. In 2007 this was improved by Martin Fürer (Fürer's algorithm)^[16] to requite a time complexity of n log(n) 2^{Θ(log*(north))} using Fourier transforms over circuitous numbers. Anindya De, Chandan Saha, Piyush Kurur and Ramprasad Saptharishi^[17] gave a similar algorithm using modular arithmetic in 2008 achieving the same running time. In context of the above material, what these latter authors take achieved is to notice N much less than two^3k + 1, so that Z/NZ has a (2m)th root of unity. This speeds up computation and reduces the time complication. However, these latter algorithms are only faster than Schönhage–Strassen for impractically large inputs.

In March 2019, David Harvey and Joris van der Hoeven appear their discovery of an O(n log due north) multiplication algorithm.^[18] It was published in the Annals of Mathematics in 2021.^[19]

Using number-theoretic transforms instead of discrete Fourier transforms avoids rounding error issues by using modular arithmetic instead of floating-signal arithmetic. In society to apply the factoring which enables the FFT to work, the length of the transform must exist factorable to small primes and must be a factor of N − ane, where N is the field size. In detail, calculation using a Galois field GF(k ^two), where k is a Mersenne prime, allows the utilise of a transform sized to a power of ii; e.m. k = 2³¹ − one supports transform sizes upwardly to ii³².

Lower bounds [edit]

There is a trivial lower jump of Ω(n) for multiplying two n-bit numbers on a single processor; no matching algorithm (on conventional machines, that is on Turing equivalent machines) nor any sharper lower bound is known. Multiplication lies outside of Air-conditioning⁰[p] for whatever prime p, meaning there is no family of constant-depth, polynomial (or even subexponential) size circuits using AND, OR, Not, and Modern _p gates that can compute a product. This follows from a constant-depth reduction of MOD _q to multiplication.^[20] Lower bounds for multiplication are also known for some classes of branching programs.^[21]

Complex number multiplication [edit]

Complex multiplication unremarkably involves four multiplications and 2 additions.

${\displaystyle (a+bi)(c+di)=(ac-bd)+(bc+ad)i.}$

Or

${\displaystyle {\begin{array}{c|c|c}\times &a&bi\\\hline c&ac&bci\\\hline di&adi&-bd\end{array}}}$

Equally observed by Peter Ungar in 1963, i can reduce the number of multiplications to three, using substantially the aforementioned computation every bit Karatsuba's algorithm.^[22] The product (a +bi) · (c +di) can be calculated in the following manner.

thou ₁ = c · (a + b)

k ₂ = a · (d − c)

k ₃ = b · (c + d)

Real part = k _i − k _iii

Imaginary part = k _one + yard ₂.

This algorithm uses only iii multiplications, rather than 4, and five additions or subtractions rather than ii. If a multiply is more expensive than three adds or subtracts, every bit when calculating by hand, then there is a gain in speed. On modernistic computers a multiply and an add can take well-nigh the same time so there may be no speed proceeds. At that place is a merchandise-off in that in that location may exist some loss of precision when using floating point.

For fast Fourier transforms (FFTs) (or whatever linear transformation) the circuitous multiplies are past constant coefficients c +di (called twiddle factors in FFTs), in which case two of the additions (d−c and c+d) can exist precomputed. Hence, but 3 multiplies and three adds are required.^[23] Still, trading off a multiplication for an addition in this style may no longer exist benign with modern floating-point units.^[24]

Polynomial multiplication [edit]

All the higher up multiplication algorithms can too be expanded to multiply polynomials. For instance the Strassen algorithm may exist used for polynomial multiplication^[25] Alternatively the Kronecker substitution technique may be used to convert the trouble of multiplying polynomials into a single binary multiplication.^[26]

Long multiplication methods can be generalised to allow the multiplication of algebraic formulae:

          14ac - 3ab + ii multiplied by air-conditioning - ab + i        

          14ac  -3ab   2    ac   -ab   ane  ————————————————————  14atwoc2          -3aiibc   2ac         -14aiibc         3 a2b2          -2ab                  14ac           -3ab   2  ———————————————————————————————————————  14a2ctwo          -17a2bc   16ac  3a2b2          -5ab  +two  =======================================[27]        

Every bit a farther instance of column based multiplication, consider multiplying 23 long tons (t), 12 hundredweight (cwt) and two quarters (qtr) by 47. This example uses avoirdupois measures: 1 t = 20 cwt, 1 cwt = 4 qtr.

          t    cwt  qtr    23     12    ii                47 ten  ————————————————   141     94   94   940    470    29     23  ————————————————  1110    587   94  ————————————————  1110      7    two  =================  Answer: 1110 ton seven cwt 2 qtr        

Get-go multiply the quarters by 47, the result 94 is written into the first workspace. Side by side, multiply cwt 12*47 = (2 + x)*47 but don't add up the fractional results (94, 470) yet. Likewise multiply 23 by 47 yielding (141, 940). The quarters column is totaled and the result placed in the second workspace (a fiddling move in this case). 94 quarters is 23 cwt and 2 qtr, then place the 2 in the respond and put the 23 in the next column left. Now add up the three entries in the cwt column giving 587. This is 29 t 7 cwt, so write the vii into the answer and the 29 in the column to the left. At present add up the tons cavalcade. There is no adjustment to brand, so the result is just copied down.

The same layout and methods can be used for any traditional measurements and non-decimal currencies such as the old British £sd system.

See also [edit]

• Binary multiplier
• Division algorithm
• Logarithm
• Mental calculation
• Prosthaphaeresis
• Slide dominion
• Trachtenberg organization
• Horner scheme for evaluating of a polynomial
• Residue number system § Multiplication for another fast multiplication algorithm, particularly efficient when many operations are done in sequence, such as in linear algebra
• Dadda multiplier
• Wallace tree

References [edit]

1. ^ "Multiplication". www.mathematische-basteleien.de . Retrieved 2022-03-xv .
2. ^ Brent, Richard P (March 1978). "A Fortran Multiple-Precision Arithmetics Bundle". ACM Transactions on Mathematical Software. four: 57–lxx. CiteSeerX10.1.1.117.8425. doi:10.1145/355769.355775. S2CID 8875817.
3. ^ Gary Eason, Dorsum to school for parents, BBC News, thirteen February 2000
   Rob Eastaway, Why parents can't do maths today, BBC News, ten September 2010
4. ^ Corlu, K. S., Burlbaw, L. Grand., Capraro, R. M., Corlu, M. A.,& Han, South. (2010). The Ottoman Palace School Enderun and The Man with Multiple Talents, Matrakçı Nasuh. Journal of the Korea Society of Mathematical Education Serial D: Research in Mathematical Education. 14(1), pp. 19–31.
5. ^ Bogomolny, Alexander. "Peasant Multiplication". www.cut-the-knot.org . Retrieved 2017-eleven-04 .
6. ^ D. Wells (1987). The Penguin Dictionary of Curious and Interesting Numbers. Penguin Books. p. 44.
7. ^ Cool Multiplication Math Fox, archived from the original on 2021-12-eleven, retrieved 2020-03-14
8. ^ McFarland, David (2007), Quarter Tables Revisited: Earlier Tables, Division of Labor in Table Construction, and After Implementations in Analog Computers, p. 1
9. ^ Robson, Eleanor (2008). Mathematics in Aboriginal Iraq: A Social History. p. 227. ISBN978-0691091822.
10. ^ "Reviews", The Civil Engineer and Architect'south Periodical: 54–55, 1857.
11. ^ Holmes, Neville (2003), "Multiplying with quarter squares", The Mathematical Gazette, 87 (509): 296–299, doi:x.1017/S0025557200172778, JSTOR 3621048, S2CID 125040256.
12. ^ Everett Fifty., Johnson (March 1980), "A Digital Quarter Square Multiplier", IEEE Transactions on Computers, Washington, DC, USA: IEEE Computer Club, vol. C-29, no. 3, pp. 258–261, doi:ten.1109/TC.1980.1675558, ISSN 0018-9340, S2CID 24813486
13. ^ Putney, Charles (Mar 1986), "Fastest 6502 Multiplication All the same", Apple Assembly Line, vol. 6, no. 6
14. ^ D. Knuth, The Art of Computer Programming, vol. 2, sec. 4.3.3 (1998)
15. ^ A. Schönhage and V. Strassen, "Schnelle Multiplikation großer Zahlen", Computing 7 (1971), pp. 281–292.
16. ^ Fürer, M. (2007). "Faster Integer Multiplication" in Proceedings of the thirty-ninth annual ACM symposium on Theory of computing, June 11–xiii, 2007, San Diego, California, USA
17. ^ Anindya De, Piyush P Kurur, Chandan Saha, Ramprasad Saptharishi. Fast Integer Multiplication Using Modular Arithmetic. Symposium on Theory of Computation (STOC) 2008.
18. ^ Hartnett, Kevin (2019-04-11). "Mathematicians Discover the Perfect Way to Multiply". Quanta Magazine . Retrieved 2019-05-03 .
19. ^ Harvey, David; van der Hoeven, Joris (2021). "Integer multiplication in fourth dimension ${\displaystyle O(n\log northward)}$ ". Annals of Mathematics. Second Serial. 193 (2): 563–617. doi:ten.4007/annals.2021.193.2.4. MR 4224716.
20. ^ Sanjeev Arora and Boaz Barak, Computational Complexity: A Modern Approach, Cambridge University Press, 2009.
21. ^ Farid Ablayev and Marek Karpinski, A lower bound for integer multiplication on randomized ordered read-once branching programs, Information and Computation 186 (2003), 78–89.
22. ^ Knuth, Donald E. (1988), The Art of Calculator Programming volume 2: Seminumerical algorithms, Addison-Wesley, pp. 519, 706
23. ^ P. Duhamel and M. Vetterli, Fast Fourier transforms: A tutorial review and a land of the art" Archived 2014-05-29 at the Wayback Machine, Betoken Processing vol. xix, pp. 259–299 (1990), department 4.one.
24. ^ Southward. G. Johnson and Yard. Frigo, "A modified divide-radix FFT with fewer arithmetic operations," IEEE Trans. Point Process. vol. 55, pp. 111–119 (2007), section IV.
25. ^ "Strassen algorithm for polynomial multiplication". Everything2.
26. ^ von zur Gathen, Joachim; Gerhard, Jürgen (1999), Modern Computer Algebra, Cambridge University Press, pp. 243–244, ISBN978-0-521-64176-0 .
27. ^ Castle, Frank (1900). Workshop Mathematics. London: MacMillan and Co. p. 74.

Further reading [edit]

• Warren Jr., Henry Due south. (2013). Hacker'south Please (ii ed.). Addison Wesley - Pearson Education, Inc. ISBN978-0-321-84268-viii.
• Savard, John J. Yard. (2018) [2006]. "Advanced Arithmetic Techniques". quadibloc. Archived from the original on 2018-07-03. Retrieved 2018-07-16 .
• Johansson, Kenny (2008). Low Ability and Low Complication Shift-and-Add together Based Computations (PDF) (Dissertation thesis). Linköping Studies in Scientific discipline and Technology (ane ed.). Linköping, Sweden: Department of Electrical Engineering, Linköping University. ISBN978-91-7393-836-5. ISSN 0345-7524. No. 1201. Archived (PDF) from the original on 2017-08-13. Retrieved 2021-08-23 . (x+268 pages)

External links [edit]

Bones arithmetic [edit]

• The Many Means of Arithmetic in UCSMP Everyday Mathematics
• A Powerpoint presentation most ancient mathematics
• Lattice Multiplication Wink Video

Advanced algorithms [edit]

• Multiplication Algorithms used by GMP

frankelalovion.blogspot.com

Source: https://en.wikipedia.org/wiki/Multiplication_algorithm

Share this post